Author:
(1) Yitang Zhang.
Table of Links
- Abstract & Introduction
- Notation and outline of the proof
- The set Ψ1
- Zeros of L(s, ψ)L(s, χψ) in Ω
- Some analytic lemmas
- Approximate formula for L(s, ψ)
- Mean value formula I
- Evaluation of Ξ11
- Evaluation of Ξ12
- Proof of Proposition 2.4
- Proof of Proposition 2.6
- Evaluation of Ξ15
- Approximation to Ξ14
- Mean value formula II
- Evaluation of Φ1
- Evaluation of Φ2
- Evaluation of Φ3
- Proof of Proposition 2.5
Appendix A. Some Euler products
Appendix B. Some arithmetic sums
Appendix B. Some arithmetic sums
Proof of Lemma 15.1. Put
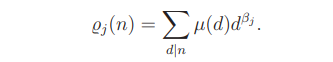
First we claim that
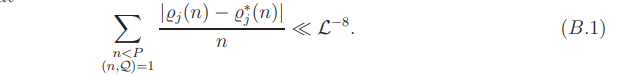
Since χ = µ ∗ ν, it follows that
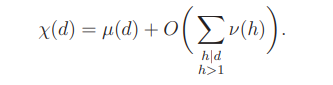
Hence
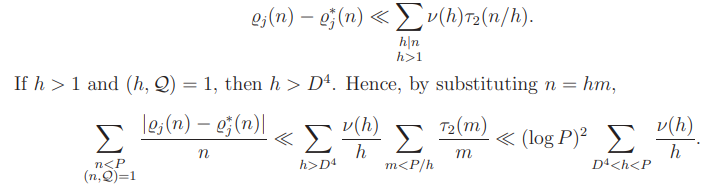
This together with Lemma 3.2 yields (B.1).
Next we claim that
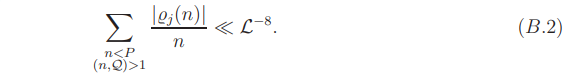
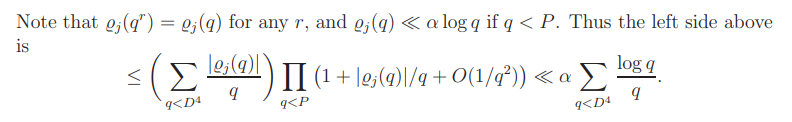
This yields (B.2).
By (B.1) and (B.2), for µ = 2, 3,
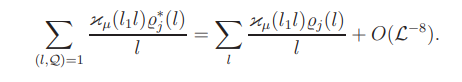
We proceed to prove theassertion with µ = 2. Since
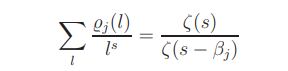
for σ > 1 and
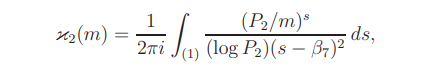
it follows that

For µ = 1 the proof is therefore reduced to showing that
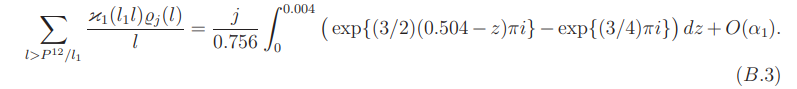
By (4.2) and (4.3), the left side of (B.3) is equal to
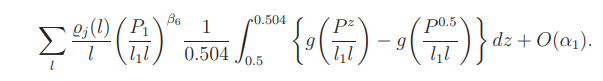
By a change of variable, for 0.5 ≤ z ≤ 0.504,
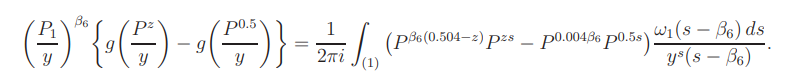
Hence, in a way similar to the proof of, we find that the left side of (B.3) i
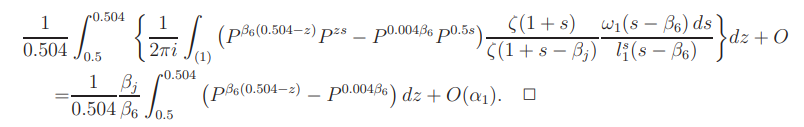
Proof of Lemma 17.1. By Lemma 3.1,
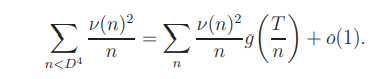
The sum on the right side is equal to
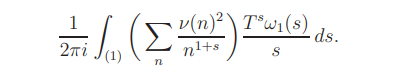
Assume σ > 1. We have
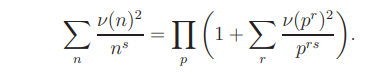
If χ(p) = 1, then (see [19, (1.2.10)])
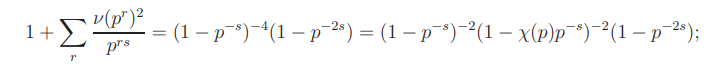
if χ(p) = −1, then
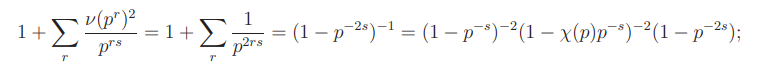
if χ(p) = 0, then
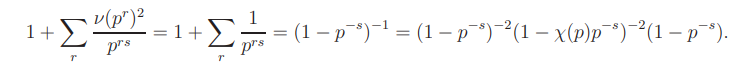
Hence
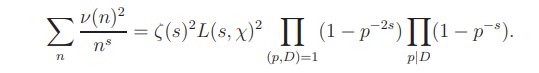
In a way similar to the proof of, by (A) and simple estimate, we find that the integral (14) is equal to the residue of the function
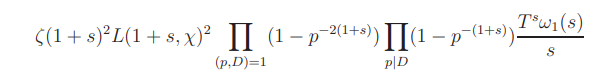
at s = 0, plus an acceptable error O, which is equal to
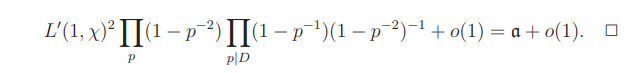
This paper is available on arxiv under CC 4.0 license.

