Author:
(1) Yitang Zhang.
Table of Links
- Abstract & Introduction
- Notation and outline of the proof
- The set Ψ1
- Zeros of L(s, ψ)L(s, χψ) in Ω
- Some analytic lemmas
- Approximate formula for L(s, ψ)
- Mean value formula I
- Evaluation of Ξ11
- Evaluation of Ξ12
- Proof of Proposition 2.4
- Proof of Proposition 2.6
- Evaluation of Ξ15
- Approximation to Ξ14
- Mean value formula II
- Evaluation of Φ1
- Evaluation of Φ2
- Evaluation of Φ3
- Proof of Proposition 2.5
Appendix A. Some Euler products
Appendix B. Some arithmetic sums
18. Proof of Proposition 2.5
By the discussion at the end of Section 2, it suffices to prove (2.32) and (2.33).
Proof of (2.32).
By (12.3), (12,17), (13.7), (15.24), (16.17) and (17.10),
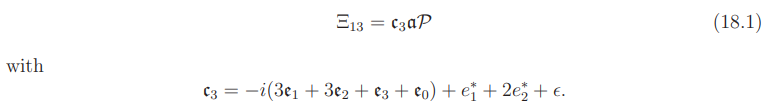
In view of (15.), we can write
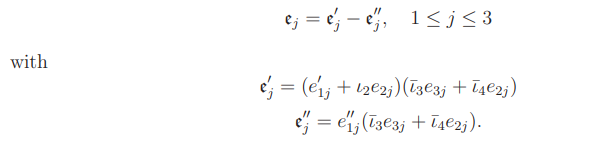
By calculation (there is a theoretical interpretation),
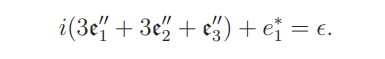
Hence
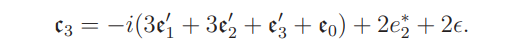
Direct calculation shows that

It follows from (8.24), (9.8) and (18.2) that
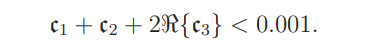
This with together (8.23), (9.7) and (18.1) yields (2.32).
Proof of (2.33).
By Lemma 8.1,
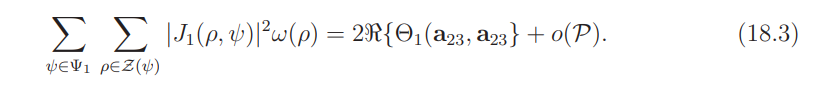
We have
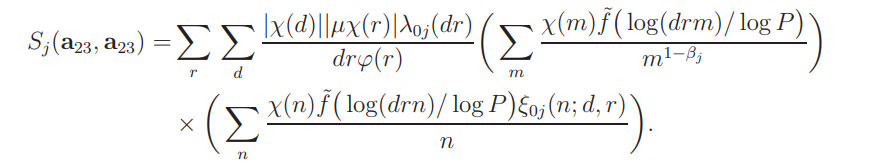
The right side is split into three sums according to
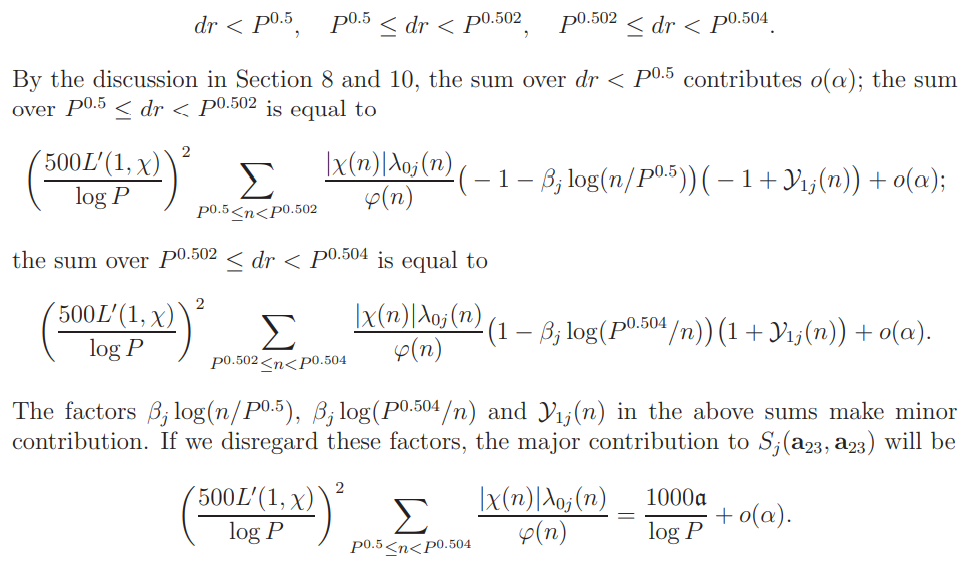
Thus we have the crude bound
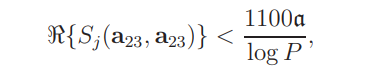
so that
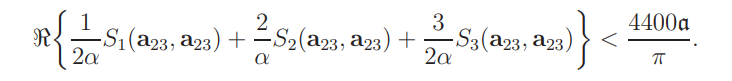
This yields (2.33) by Lemma 8.1 and Proposition 7.1
This paper is available on arxiv under CC 4.0 license.

